Lord Larehip

It's looking that way.

Janszoon

That's pretty exciting! I mean, I knew Billy Idol posted here, for obvious reasons, but this revelation really takes things to another level.

__________________
A Night in the Life of the Invisible Man

Time & Place

25 Albums You Should Hear Before the Moon Crashes into the Earth and We All Die

last.fm

Lord Larehip

Why don't you get Tom Waits to post here?

Janszoon

He used to.

__________________
A Night in the Life of the Invisible Man

Time & Place

25 Albums You Should Hear Before the Moon Crashes into the Earth and We All Die

last.fm

GOATPOP

Tom Waits has better parties to crash brother.

NGPercussion

Music theory is incredibly interesting. Was talking with a theory professor at one time about a Béla Bartók piece, and he discussed how the piece modulates to perpendicular keys at times, rather than just relative or parallel keys. Very interesting stuff.

Lord Larehip

The Circle of Fifths also unites music and geometry in a number of ways and we'll investigate one of them here.

How can you construct the proper diatonic scales from each note on the circle?

There are a number of ways. Chords are said to consist of root, third and fifth. But that scheme, although widely used, is not particularly useful. I was classically trained on the double bass and we construct chords in thirds only: root, major third and then another minor third on top of that for a major chord or root, minor third and then a major third on top for a minor chord. Using this method, let’s construct our diatonic scales on the Circle of Fifths using the pattern shown above: root, major 3rd, minor 3rd, major 3rd, minor 3rd, minor 3rd, major 3rd, minor 3rd.

For example, let us use C. Starting at C we go up a major 3rd (or 4 half-steps) to E. Then go up a minor 3rd (or 3 half-steps) to G. Then go up another major 3rd to B. Then another minor 3rd to D. Then another minor 3rd to F. Then a major 3rd to A. Then a minor 3rd to C'. So the order is:

C E G B D F A C'


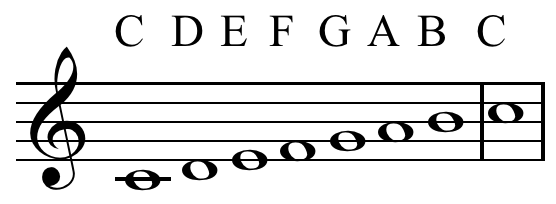
Basically, you're starting at C and skipping a note to E, skipping another to G, skipping another to B then going back and starting at D and repeating the pattern.

Now arrange these notes starting at C in a circle in alphabetical order: C (C') D E F G A B and draw lines starting from C to each note in the order obtained in the sequence shown above. You get a 7-pointed star! And this works with any key and whether major or minor. Try it!



Pick another key—say Ab. The order we obtain is:

Ab C Eb G Bb Db F Ab'

Now lay them in a circle in alphabetical order and then draw a line from one note to the next in the sequence above—a 7-pointed star!

Lord Larehip

Or we can make a circle of the notes in the original sequence Ab C Eb G Bb Db F and then connect the notes alphabetically with lines to obtain a completely different type of 7-pointed star.



Pythagoras was right!

What is also noteworthy is that the sequence of the C scale by thirds--C E G B D F A--contains how the notes are laid out on manuscript paper. FACE represents the spaces between the lines on the treble staff and EGBDF represents the staff lines themselves. Needless to say, it also describes the layout of the bass staff: ACEG GBDFA respectively.

But what's even more noteworthy is that no matter what scale on the Circle we plot out, the order of the notes follows that layout if we ignore the accidentals for the moment. For example, the Ab flat scale:

Ab C Eb G Bb Db F

Ignore the accidentals and there it is again ACE GBDF

Pick another scale—say F:

F A C E G Bb D F'

And there it is again: FACE EGBDF

It will always work out that way. It will always show the layout on staff paper and form a 7-pointed star. Doesn’t matter if you use the equivalent minors and it doesn’t matter if you use enharmonic equivalents. It always produces the same pattern.

Lord Larehip

Is the star a coincidence? Let’s see if it works with the Chinese pentatonic scale. This scale is generated by starting with the note called gong which drops a 4th to zhi which rises a fifth to shang then drops a fourth to yu then rises a fifth to jue. From lowest to highest, the notes are zhi, yu, gong, shang and jue.

Now, make a circle and space these notes out equally along the perimeter (72 degrees apart) in the order of their generation--gong, zhi, shang, yu and jue--and connect them with lines in order going from lowest note to highest--zhi, yu, gong, shang and jue. What geometrical figure do you get? This one:



Or we can reverse the layout and mark the perimeter of the circle with the notes in order from lowest to highest and connect them with lines in the order of their generation and we will get the identical pentagram again.

Lord Larehip

Are the pentatonic (5-note) and diatonic (7-note) scales related? Yes, intimately.

Now, if you go to the Circle of Fifths and connect every 5th or 7th mark with a line you will get the identical geometrical figure:



We could also make a 12-sided polygon if we connect every mark in sequence or by counting by 11s. If we count by any other intervals, however, we will not hit all 12 marks on the circle. They will form only squares, triangles or hexagons. Why is that? Because a 4th is 5 half-steps, a 5th is 7 half-steps, a minor second is 1 half-step and a major 7th is 11 half-steps, and the octave is 12 half-steps. 1, 5, 7 and 11 are what we say in mathematical jargon co-prime in modulo 12. That is, they are not divisible with any number other than 1 and themselves and also not factors of 12. All the other intervals are not prime or are factors of 12 or both and so end up creating circles that are factors of 12 but never all 12.

Geometrically, a Circle of 5ths should be a large 12-pointed star with a smaller 7-pointed star at each of the 12 points.