Okay, okay. So the circle can show you how to determine a key based on the number of sharps of flats. But can it tell us which notes are sharped or flatted in each key signature? Yes, it can.
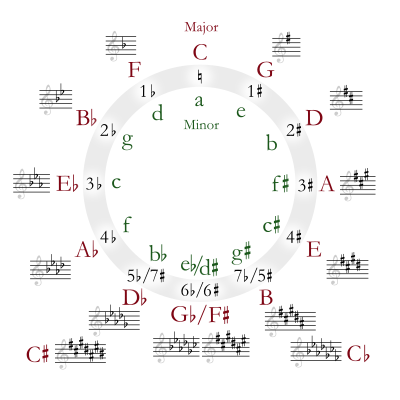
Use the above figure for reference. To determine the flats, drop back two notes on the circle. G major gets one sharp so drop back two spaces on the circle to F major and that is the note that gets sharped in G major. Trigonometrically, draw a line from G to the center of the circle and go 60 degrees counterclockwise (remember that each note represents 30 degrees of arc). Moving to D major, which has two sharps, drop back 60 degrees to C and that is the next sharp so D major has two sharps—F and C. And so on.
For flats, we look at the note on the opposite side of the circle. So the note opposite F is B so that is the note that gets flatted in F major. Trigonometrically, we drop back (or move forward) 180 degrees to find the flats. The next note of the circle is Bb and will get two flats. We already know that one will be B and the other is 180 from Bb which is E so Bb major is flatted at B and E. And so on.
The special case is C which has no key signature (no sharps or flats). If we drop back 60 degrees as in the manner of finding sharps, we find ourselves at Bb which, if sharped, simply becomes B. Or if we cross the circle 180 degrees to find the flats, we end up at Gb, which, if flatted, simply becomes F. So, as the circle shows, C has no naturally occurring sharps or flats.